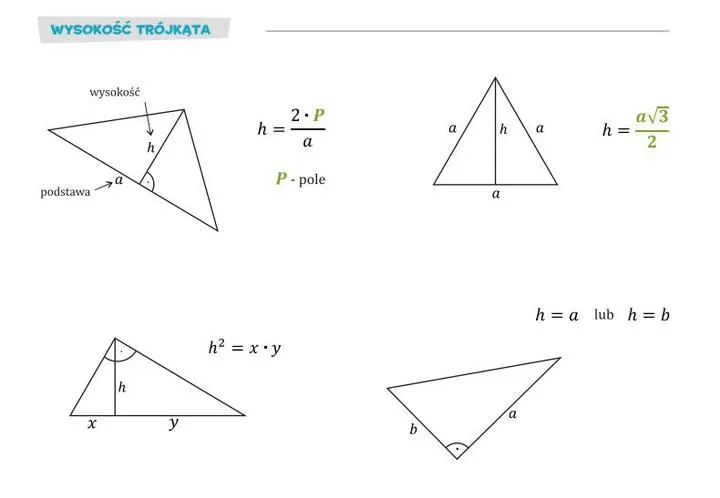
W geometrii wysokie będą nie tylko budynki, lecz także trójkąty! Wysokość trójkąta to linia, która opuszcza wierzchołek trójkąta prostopadle na bok przeciwny. Należy jednak zaznaczyć, że nie mówimy tu o kręceniach i akrobacjach, chociaż mogłoby to być dość widowiskowe. Wysokość umożliwia zrozumienie działania trójkątów oraz przyswajanie różnych formuł związanych z polem. W końcu warto przyznać, że bez odpowiedniej wysokości nie zyskamy efektownego trójkąta!
Gdy już mamy ogólny zarys, nadszedł czas na zrozumienie różnic w wysokościach w zależności od typu trójkąta. W trójkącie prostokątnym, wysokość pokrywa się z jedną z krawędzi, co sprawia, że można ją uznać za "wyższej jakości". Z kolei w trójkącie ostrokątnym i rozwartokątnym sytuacja zmienia się, ponieważ wysokości muszą opadać poza dodanymi bokami. Wygląda to trochę jak taniec: w niektórych przypadkach można po prostu zapisać się na kurs tańca, w innych trzeba improwizować! Jednak to dopiero początek naszej przygody z geometrią.
Jak znaleźć wysokość trójkąta?
Oto świetna wiadomość! Możemy obliczyć wysokość! Wystarczy znać pole trójkąta oraz długość podstawy. Wykorzystajcie wzór: pole = (1/2) * podstawa * wysokość. Dzięki kilku algebraicznym sztuczkom odkryjemy tajemniczą wysokość, która każdemu trójkątowi doda charakteru! Rzeczywiście, geografia uliczna każdego miasta może się schować przy tak zwanym „trójkątnym wyzwaniu”!
Ostatnio zrozumieliśmy, że trójkąty to nie tylko nudne figury geometryczne, lecz także prawdziwi mistrzowie stylu. W każdym przypadku, gdy spotykasz się z trójkątem, pamiętaj, że każdy z nich ma swoją wysokość, historię i wyzwania. Dlatego zarówno w nauce, jak i w życiu – nie bój się zmierzyć z wyzwaniem prosto na bok i odkrywać wysokości w każdej sytuacji!
Krok po kroku: Jak prawidłowo narysować wysokość w różnych rodzajach trójkątów
Nie ma nic lepszego od rozgrzewki przed rozpoczęciem rysowania! Gdy zgłębiamy temat rysowania wysokości w trójkątach, najlepiej zacząć od trójkątów prostokątnych. Te wszystkie dobrze znane i lubiane figury geometryczne! Wystarczy znaleźć kąt prosty, a następnie opuścić linię do przeciwległego boku – i voilà! Wysokość pojawi się jak za dotknięciem czarodziejskiej różdżki, a efekty okazują się łatwe do oszacowania. Pamiętaj, aby nigdy nie zapominać o kącie 90 stopni, gdyż to klucz do sukcesu! Jeśli Twoja linia nie wygląda na prostokątną, możesz z powodzeniem udawać, że tworzysz nowoczesną sztukę abstrakcyjną.
Przechodzimy teraz do trójkątów ostrokątnych, które tylko czekają na to, aby pokazać, jakie mają możliwości. W tym przypadku sytuacja staje się jeszcze prostsza! Wybierz dowolny bok, a następnie pozwól, aby ręka prowadziła Cię w dół ku stronie przeciwległej. Uwierz, że efekt będzie lepszy, gdy skupisz się na kącie. Wysokość w ostrokątnym trójkącie może przypominać artystę malującego na płótnie – polegaj na sobie i swoich umiejętnościach! Podczas rysowania poczujesz, że stajesz się twórcą, więc rób to z gracją.
Wysokość w trójkącie rozwartokątnym: Nie ma zmiłuj!
Oto nastał czas na omówienie naszego ostatniego bohatera, czyli trójkąta rozwartokątnego. W tym przypadku zabawa dopiero się zaczyna! Wysokość musi pokonać długą drogę, a co więcej, znajduje się na zewnątrz trójkąta. Jakie szaleństwo! Wybierając punkt na podstawie i rysując linię do wierzchołka, pamiętaj o precyzji – konieczna jest dokładność jak u chirurga. Gdy już to zrobisz, poczujesz się jak MVP matematyki, a każdy, kto spojrzy na Twoje dzieło, może pomyśleć, że jesteś geniuszem geometrii.
Podsumowując, rysowanie wysokości w różnych rodzajach trójkątów to doskonały sposób na odkrywanie tajników geometrii. Nie traktuj tego procesu jako zbyt trudnego – potraktuj go jak przygodę, w której odgrywasz główną rolę. Nie zapominaj o linijce, ale także odrobina fantazji zawsze się przyda! Nawet jeśli coś nie wyjdzie na kartce, pamiętaj, że każdy mistrz kiedyś był amatorem. Rysuj, celebruj swoje postępy i baw się dobrze – w końcu chodzi tylko o trójkąty!
Oto kilka kluczowych informacji o rysowaniu wysokości w różnych rodzajach trójkątów:
- W trójkącie prostokątnym wysokość jest łatwa do wyznaczenia przy użyciu kąta 90 stopni.
- W trójkącie ostrokątnym można wybierać dowolny bok jako podstawę do rysowania wysokości.
- W trójkącie rozwartokątnym wysokość znajduje się na zewnątrz figury.
Praktyczne zastosowania: Wysokość w trójkącie w zadaniach matematycznych
Wysokość w trójkącie to nie tylko nowa fryzura, którą można zaprezentować na szkolnym balu. To także istotny element wykorzystywany w matematycznych zmaganiach. Kiedy słyszymy to słowo, niektórzy wyobrażają sobie niewidzialną linię przecinającą trójkąt, podczas gdy inni marzą o zdobyciu złotej gałązki z tytułem „królowej matematyki”. W rzeczywistości, wysokość trójkąta to odcinek łączący wierzchołek z przeciwległym bokiem, a co najważniejsze, jest do niego prostopadły. Tak oto pojawia się pytanie: jak możemy wykorzystać tę wiedzę w praktyce? Odpowiedź znajdziemy w zadaniach matematycznych!
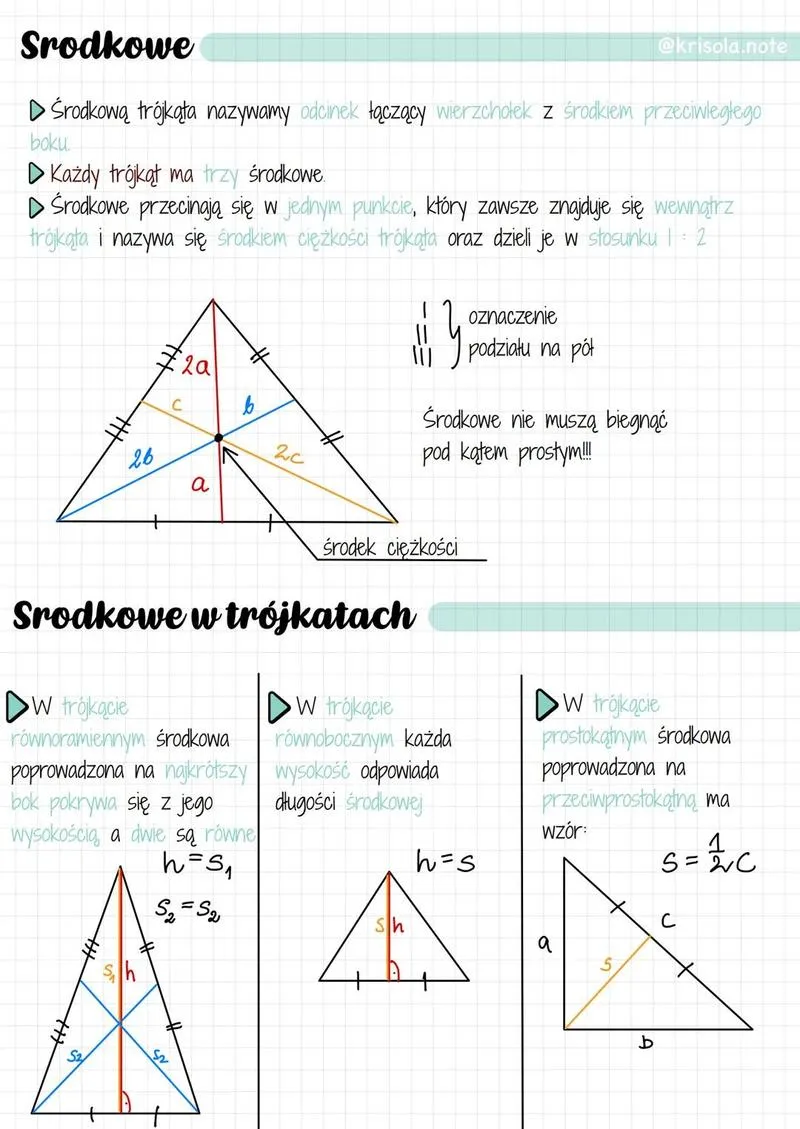
Gdy omawiamy trójkąty, wysokość pełni kluczową rolę w obliczaniu pola. Jednakże to nie wszystko! Kto chciałby pozostać bez rezultatów, rozwiązując problem wymagający wykorzystania podstawy trójkąta? Wszyscy pragną przecież stać się przyszłymi Einsteinami! Wystarczy zastosować wzór: pole = (podstawa * wysokość) / dwa. Prawda, że to proste? Choć może to brzmieć zwyczajnie, metoda ta nie tylko ułatwia praktyczne rozwiązywanie zadań, ale także pozwala wykazać, jak dobrze przyswoiliśmy teorię trójkątów.
Wysokość jako narzędzie w różnych kontekstach
Rozpocznijmy teraz wyobrażeniem sytuacji, w której organizujemy piknik w kształcie trójkąta. Na piknik przychodzą wszyscy znajomi: kocyk rozłożony na trawie, słońce świeci, a my rozpoczniemy mądrą dyskusję na temat wysokości w trójkątach. W międzyczasie musimy jednak ustalić, jaką przestrzeń zajmie nasza biesiada. Bez obaw! Wystarczy obliczyć wysokość odpowiedniego trójkąta i voila! Ustalamy, ile pysznych przekąsek pomieści nasz trójkątny kocyk. Trójkąty w praktyce? To prawdziwa przyjemność!
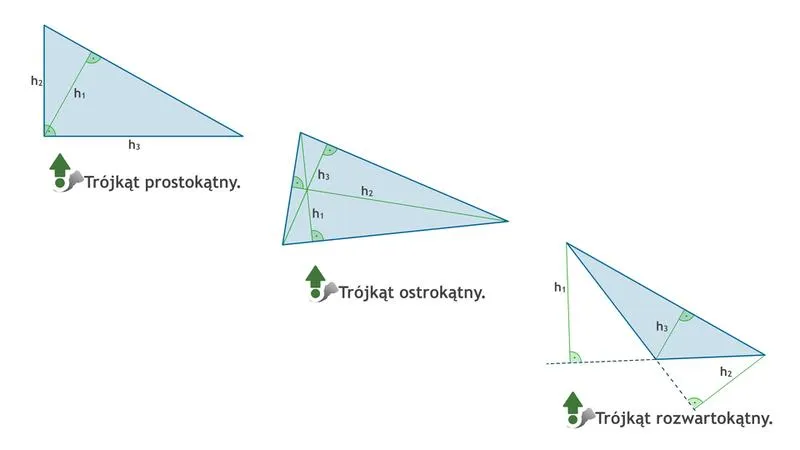
Nie zapominajmy również, że różne rodzaje trójkątów wprowadzają swoje specyficzne smaczki. Wysokość w trójkącie prostokątnym często okazuje się łatwiejsza do znalezienia, natomiast trójkąty ostrokątne mogą zaskoczyć swoimi szczegółami. A co z trójkątami rozwartokątnymi? Tutaj warto być czujnym, gdyż wysokość może „uciekać” poza ich granice. Z matematyki można wyciągnąć wiele kolorowych wniosków i zastosowań, co sprawia, że zadania o wysokości w trójkącie zamieniają się w prawdziwą intelektualną zabawę!
| Aspekt | Opis |
|---|---|
| Definicja wysokości w trójkącie | Odcinek łączący wierzchołek z przeciwległym bokiem, prostopadły do tego boku. |
| Rola wysokości w zadaniach matematycznych | Kluczowa w obliczaniu pola trójkąta. |
| Wzór na pole trójkąta | pole = (podstawa * wysokość) / 2 |
| Przykład zastosowania | Obliczenie wysokości w kontekście pikniku w kształcie trójkąta. |
| Rodzaje trójkątów | Wysokość w trójkącie prostokątnym jest łatwiejsza do znalezienia, natomiast w ostrokątnych i rozwartokątnych mogą być trudności. |
Czy wiesz, że wysokość w trójkącie rozwartokątnym nie tylko "ucieka" poza jego granice, ale także może być trudna do zauważenia w kontekście dalszych obliczeń? W takich przypadkach warto wykorzystać inne właściwości trójkąta lub skorzystać z metod prostokątnych, aby ułatwić sobie zadanie!
Ilustracje i techniki: Wizualizacja wysokich linii w geometrii
Można pomyśleć, że geometria sprowadza się jedynie do prostych figur, kątów oraz linii. Jednak gdy zaczynamy zgłębiać ten temat, odkrywamy, że skrywa on prawdziwe skarby! Dziś porozmawiamy o wysokich liniach w geometrii, a szczególnie skupimy się na ich wizualizacjach. Zanim przejdziemy dalej, spieszę z wyjaśnieniem, co właściwie oznacza termin „wysoka linia”! Otóż to najwyższy punkt, który można opuścić na bok figury. W przypadku trójkąta o różnorodnych kształtach te wysokie linie prowadzą do zupełnie innych rezultatów. Z pewnością warto zauważyć, że każda wysokość ma swoje unikalne cechy i odsłania, co tak naprawdę kryje się w tym figuralnym świecie.
Wizualizacja tych linii nie ogranicza się jedynie do prostego rysowania. To swoisty taniec punktów i kątów, który umożliwia dostrzeganie relacji między figurami oraz ich właściwościami. Rysując trójkąt, natychmiast przystępujemy do rysowania jego wysokości. Na przykład w wypadku trójkąta ostrokątnego, z trzema pięknymi wysokościami, nasza kartka staje się areną geometrycznych zmagań! Jak zatem wygląda sytuacja w przypadku trójkąta prostokątnego? Tam jedna wysokość szczególnie „wznosi się”, gdyż dotyka 90 stopni. Oczywiście wspomnienie o kątach nie pojawia się przypadkowo – w końcu nie warto krytykować geometrii, aby przyciągnąć uwagę słuchaczy.
Jak rysować wysokości w praktyce?
Aby efektywnie wizualizować te geometryczne zawirowania, warto wykonać kilka ćwiczeń! Na początek narysuj trójkąt: niech będzie kolorowy, dla lepszego efektu! Następnie weź linijkę i zmierz wysokości. Pamiętaj, aby nie wyznaczać ich w błędny sposób, bo to tak, jakbyś próbował przygotować sushi bez ryżu. Wysokości powinny prowadzić do konkretnych punktów, czyli węzłów w trójkącie, co sprawia, że każdy utwór geometryczny staje się bardziej harmonijny. A jeżeli twoje rysunki czasami przypominają bardziej dzieła Picassa niż Euclidesa, nie martw się! Każdy wielki artysta zaczynał od zera. Najważniejsze to czerpać radość z geometrii i dodawać odrobinę własnej kreatywności.
Na zakończenie pamiętajmy, że każdy kształt skrywa swoje tajemnice. Wysokie linie to tylko jedna z wielu tajemnic, a ich wizualizacje mogą prowadzić nas do niesamowitych odkryć. Oto niektóre z cech wysokich linii w geometrii:
- Prowadzą do węzłów w trójkącie.
- Ich długość różni się w zależności od rodzaju trójkąta.
- W trójkącie prostokątnym jedna wysokość dotyka kąta prostego.
Geometryczne figury stają się piękniejsze, gdy obdarzymy je szczyptą artystycznej wizji. Dlatego bierzcie kartki, ołówki i ruszajcie w drogę! A jeśli kiedykolwiek poczujecie się zagubieni w tej geometrycznej dżungli, po prostu spójrzcie na swoje „wysokie linie” – one zawsze tam czekały, gotowe, by pokazać wam drogę do matematycznego sukcesu.
Pytania i odpowiedzi
Co to jest wysokość w trójkącie?
Wysokość w trójkącie to linia, która opuszcza wierzchołek trójkąta prostopadle na bok przeciwny. Jest kluczowym elementem w obliczaniu pola trójkąta oraz pomaga zrozumieć różne właściwości tej figury geometrycznej.
Jak rysować wysokości w trójkątach prostokątnych?
Aby narysować wysokość w trójkącie prostokątnym, wystarczy znaleźć kąt prosty i opuścić linię do przeciwległego boku. Pamiętaj o zachowaniu kąta 90 stopni, ponieważ to klucz do sukcesu w tym zadaniu.
Co różni wysokości w trójkątach ostrokątnych od rozwartokątnych?
W trójkącie ostrokątnym wysokości są rysowane wewnątrz figury, podczas gdy w trójkącie rozwartokątnym wysokości muszą opadać poza jego granice. To sprawia, że rysowanie wysokości w trójkątach rozwartokątnych może być bardziej skomplikowane.
Jak można obliczyć wysokość trójkąta?
Aby obliczyć wysokość trójkąta, wystarczy znać pole trójkąta oraz długość podstawy i zastosować wzór: pole = (1/2) * podstawa * wysokość. Przykładowe przekształcenie wzoru pozwala na wyznaczenie wysokości.
Jakie praktyczne zastosowania ma wysokość w trójkącie?
Wysokość w trójkącie jest wykorzystywana nie tylko w geometrii, ale również w praktycznych zadaniach matematycznych, na przykład do obliczania pola figury. Ponadto wysokości w trójkątach mają zastosowanie w architekturze i inżynierii do obliczeń związanych ze stabilnością budowli.