Symetria w geometrii to temat, który nadaje matematyce piękno oraz, co najważniejsze, zrozumiałość. Dzieje się tak, ponieważ dzięki symetrii możemy dzielić figury na równe części, które stanowią lustrzane odbicie samych siebie. Należy zauważyć, że spotykamy symetrię nie tylko w przyrodzie, ale także w codziennym życiu – wystarczy spojrzeć w lustro, aby dostrzec nasze twarze! Kto nie pragnie być symetryczny? Bez względu na to, czy jesteś kwadratem, kołem, czy przypadkowym trójkątem, z pewnością znajdziesz swój oś symetrii, tak jak w tańcu w parach, gdzie każdy krok posiada swój przeciwległy odpowiednik!
- Symetria w matematyce nadaje piękno i zrozumiałość figurom geometrycznym.
- Rodzaje symetrii obejmują symetrię osiową, środkową oraz promienistą.
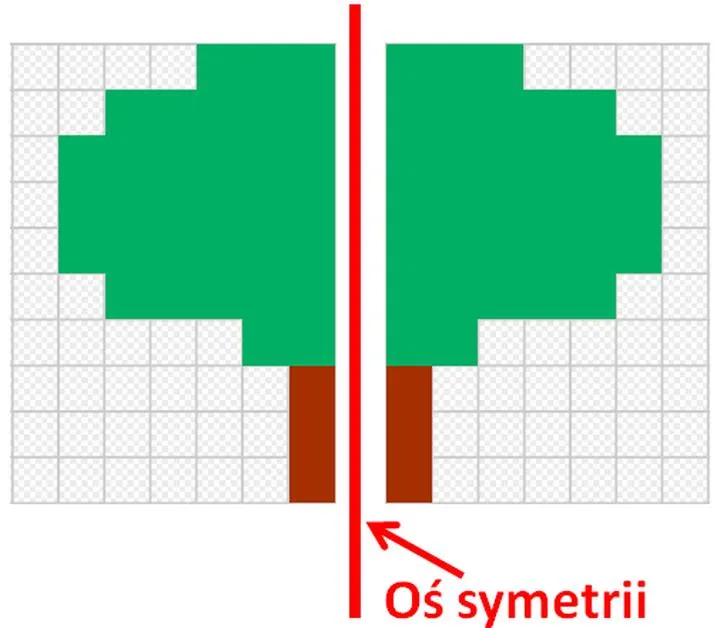
- Symetria osiowa to linia, względem której figura jest lustrzanym odbiciem.
- Symetria środkowa polega na odzwierciedleniu punktów względem środka symetrii.
- Symetria w algebrze upraszcza rozwiązywanie równań i wykrywanie wzorców.
- Symetria odgrywa kluczową rolę w sztuce, tworząc harmonijne kompozycje.
- Symetria w naturze przejawia się w roślinach i organizmach, takich jak motyle czy ryby.
- Symetria wpływa na estetykę wykresów oraz architektoniczne elementy, np. kolumny w świątyniach.
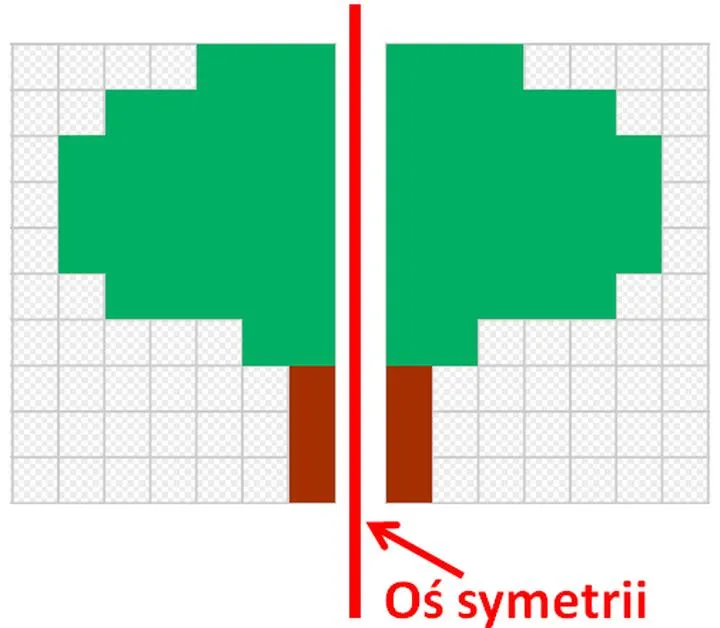
Przechodząc teraz do bardziej technicznych szczegółów, warto wspomnieć o symetrii osiowej, która w skrócie odzwierciedla strukturę na odcinku. Choć może się wydawać, że brzmi to jak coś związane z teatrem, oś symetrii to po prostu linia, względem której figura prezentuje symetrię. Wyobraź sobie, że rysujesz prostą linię – w tym przypadku każdy punkt figury z jednej strony zostaje 'przeniesiony' na drugą stronę w sposób, który zapewnia równą odległość od linii. Na przykład, trójkąt równoramienny posiada jedną oś symetrii, natomiast kwadrat może pochwalić się aż czterema! Widać zatem, że niektóre figury cieszą się większą radością z symetrii niż inne, co jest fascynujące, ponieważ życie byłoby nudne, gdyby wszystkie kształty były identyczne.
Rodzaje symetrii w geometrii

Nie należy zapominać o symetrii środkowej, która polega na odzwierciedleniu punktu w odniesieniu do innego punktu, nazywanego środkiem symetrii. Zastanawiając się nad punktem O jako centrum naszej geometrycznej galaktyki, zauważ, że każdy punkt A ma swojego bliźniaka A', znajdującego się w tej samej odległości od O, lecz po drugiej stronie. To przypomina najbardziej romantyczny taniec, w którym każdy uczestnik ma swojego partnera. Dzięki tej symetrii możemy tworzyć skomplikowane konstrukcje, które wyglądają zjawiskowo, mimo że w rzeczywistości potrafią być bardzo proste!
Warto więc pamiętać, że symetria stanowi klucz do odkrywania tajemnic geometrycznych i, co najważniejsze, może być w zasięgu naszych kredek oraz umysłów. Bez względu na to, czy rysujesz figury w pracy domowej, czy projektujesz nowy produkt, należy włączyć to wspaniałe narzędzie do swojego arsenału. Symetria przypomina supermoc w świecie matematyki, ponieważ sprawia, że wszystko staje się jaśniejsze i lepiej uporządkowane! Teraz, gdy masz tę wiedzę, upewnij się, że wykorzystasz swoje nowo nabyte umiejętności, aby tworzyć nie tylko piękne rysunki, ale także wspaniałe wspomnienia pełne symetrii w codziennym życiu.
Symetria w algebra: Jak oddziaływanie z równaniami tworzy harmonię
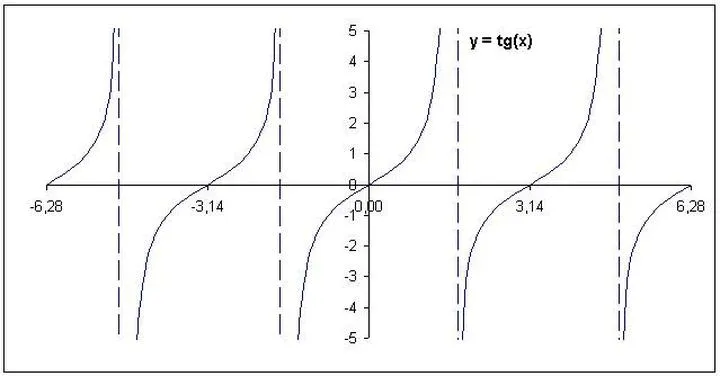
Symetria w algebrze stanowi niezwykle fascynujący temat. Choć może wydawać się stworzona przez tajemniczego naukowca w laboratorium, w rzeczywistości to bardzo przyjemny i ciekawy koncept. Wyobraź sobie, że posiadasz równanie, np. funkcję kwadratową. Kiedy spojrzysz na jej wykres, łatwo zauważysz, że istnieje oś symetrii, dzieląca go na dwie identyczne części. Ta magia symetrii sprawia, że równania przybierają nie tylko skomplikowany, ale także piękny charakter! Można to porównać do algebry, która założyła elegancką suknię i zaprosiła wszystkich na taniec.
Triki z natychmiastowym przekształceniem
Symetria nie tylko upiększa matematykę, ale także upraszcza wiele sytuacji. Dzięki niej podczas rozwiązywania równań możemy "przeskakiwać" do wyników, wykorzystując symetryczne właściwości. Na przykład, jeśli nasza funkcja symetrycznie rozkłada się względem jednej osi, wystarczy, że skupimy się na jednej stronie osi i podwoimy uzyskane wyniki! To jak odkrycie, że w twoim ulubionym miejscu na świeżym powietrzu znajduje się podwójny zestaw krzesełek — wystarczy usiąść na jednym i cieszyć się widokiem z obu stron.
Układ równań z symetrycznym twistem
W algebraicznych układach równań symetria odgrywa istotną rolę. Umożliwia dostrzeganie pewnych wzorców, co z kolei prowadzi do osiągania efektywnych rozwiązań. Na przykład, układ równań o symetrycznej formie może odsłonić tajemnice dotyczące wspólnych rozwiązań, które często zaskakują. To jak w grach planszowych — dobrze ustawione pionki potrafią dostarczyć zaskakujących zwrotów akcji, które mogą prowadzić do triumfu lub porażki. W każdym razie, algebra i symetria zawsze utrzymują nas w napięciu, oferując wiele możliwości!
- Symetria ułatwia rozwiązywanie równań.
- Umożliwia dostrzeganie wzorców w układach równań.
- Może prowadzić do zaskakujących wspólnych rozwiązań.
- Dodaje estetyki do matematycznych wykresów.

Na koniec symetria w algebrze nie stanowi jedynie efektu wizualnego – to prawdziwa siła napędowa, która pozwala maksymalnie wykorzystać potencjał równań.
Pokonując kolejne matematyczne przeszkody, pamiętaj, że symetria wspiera cię w tym skomplikowanym tańcu liczb. Kto powiedział, że matematyka nie może być piękna, harmonijna i pełna radości? Czas na założenie matematycznych butów tanecznych i wyruszenie w tę pasjonującą podróż!
Symetria w analizie matematycznej: Rola funkcji i ich właściwości
Symetria to temat, który w matematyce zyskuje na zainteresowaniu, aż można by pisać o nim całe tomy. Jednak nie martwcie się — nie zmarnujemy waszego cennego czasu! Zamiast tego podejdźmy do tego w luźny sposób. Symetria osiowa, co sugeruje sama nazwa, polega na odzwierciedleniu figur względem konkretnej osi. Wyobraźcie sobie, że każda figura to celebryta, a oś symetrii to paparazzi, którzy robią zdjęcia z obu stron. Dzięki temu, co dostrzegamy z lewej, widzimy też z prawej. W ten sposób te wszystkie trójkąty, prostokąty czy koła stają się lustrzanym odbiciem, a punkty na osi pełnią rolę punktu stałego symetrii. Prosto i pięknie, prawda?
Przejdźmy teraz do symetrii środkowej, która działa niczym najbardziej przyjacielski DJ. Wyobraźcie sobie, że zaprasza wybrane punkty do tańca. Każdy punkt występuje z partnerem, którym jest jego symetryczny odpowiednik, a wspólne miejsce spotkania to środek symetrii. Gdyby przenieść to na nasze codzienne życie, można wyobrazić sobie, że stajecie się swoimi własnymi lustrzanymi odbiciami, tańcząc w idealnej synchronizacji. Ciekawe, jak by to wyszło, prawda? Pamiętajmy jednak, że symetria w matematyce to nie tylko zabawa, ale także sposób na zrozumienie bardziej złożonych struktur oraz ich działań.
Funkcje a symetria: Jak to działa?
Teraz przyszedł czas na sekret: funkcje również posiadają swoje symetrie! Niektóre z nich to prawdziwi mistrzowie harmonii. Funkcje parzyste, na przykład, przypominają siostry bliźniaczki — zawsze pozostają takie same, gdyż spełniają warunek f(-x) = f(x). Wracając do głównego tematu, symetria w funkcjach otwiera drzwi do wielu wyjątkowych właściwości, które mogą zaskoczyć niczym najlepsze sztuczki iluzjonistyczne. Natomiast funkcje nieparzyste, zmieniając znak x, również zmieniają swoje wartości. Gdyby matematyka była festiwalem, to symetria i jej odpowiedniki z pewnością znalazłyby się w gronie najjaśniejszych punktów programu!

W matematyce symetrię można postrzegać jak magię, ponieważ działa na wszystkie „obiekty” w uniwersum liczb, figur oraz równań, pozwalając im układać się w perfekcyjną harmonię. To jak idealnie zgrana ekipa w teatrze, gdzie każdy aktor odgrywa swoją rolę, a wszystkie działania prowadzą do wspólnego celu. Ostatecznie symetria nie tylko wzbogaca analizę matematyczną, ale także sprawia, że staje się ona znacznie bardziej estetyczna i przystępna. Zatem następnym razem, gdy usłyszycie o symetrii, pamiętajcie, że to nie tylko kącik matematyki, ale także świetna zabawa!
Symetria w sztuce i naturze: Inspiracje matematyczne w świecie wokół nas
Symetria przypomina urokliwy kocyk, który pokrywa chaotyczny świat, sprawiając, że staje się on bardziej zorganizowany i estetyczny. Przyglądając się otaczającej nas naturze, dostrzegamy hipnotyzującą obecność symetrii. Od liści na drzewach po wzory na muszlach, symetria przenika każdy zakątek życia. Dlatego w sztuce i architekturze tak chętnie sięgamy po te matematyczne wzory, które nie tylko przyciągają wzrok, ale również dostarczają duchowej harmonii. Można odnieść wrażenie, że każda symetryczna figura ma swoją własną melodię, a my z niecierpliwością czekamy, żeby ją usłyszeć!
Symetria przybiera różne oblicza, a jednymi z najpopularniejszych są symetria osiowa i środkowa. Warto zrozumieć, że oś symetrii stanowi linię, względem której figura może zostać efektywnie "zreflectowana", co oznacza, że pojawia się w lustrzanym odbiciu. Na przykład trójkąt równoboczny, z dumą pokazujący swoje idealnie rozłożone boki, posiada aż trzy osie symetrii. Nie można jednak zapominać, że nie tylko figury geometryczne uczestniczą w tym matematycznym tańcu. Klasyczne rozetki w architekturze gotyckiej z powodzeniem wypełniają kościoły pięknem, które można podziwiać przez setki lat!
Symetria w sztuce: Zalety i zastosowania
Sztuka korzysta z symetrii niczym kucharz z przypraw, w efekcie tworząc niesamowite efekty wizualne i emocjonalne. Symetryczne kompozycje przyciągają wzrok oraz skłaniają nas do głębszej refleksji. Malarze, od renesansu po nowoczesność, wykorzystywali te matematyczne zasady, aby wzbogacić swoje dzieła. Chociaż obrazy Picassa czy dzieła Kandinskiego mogą wydawać się pełne chaosu, to w ich twórczości kryje się metoda oraz pewna forma symetrii! Można to porównać do sprawnego zespołu muzycznego – każdy członek wykonuje swoją rolę, a razem tworzą harmonię dźwięków, które brzmią wyjątkowo. Gdyby zabrakło symetrii, mielibyśmy do czynienia jedynie z przypadkowym hałasem.
Ciesząc się widokiem pięknie symetrycznych roślin, podziwiając klasyczne dzieła sztuki lub napotykając wzory w codziennym życiu, odkrywamy, że symetria niewidocznie nadaje sens i porządek naszemu światu. Choć niektórzy mogą sądzić, że matematyka jest surowa i bezosobowa, to jednak jej delikatniejsza strona ujawnia się, przekształcając się w coś, co rozgrzewa nasze serca oraz wzbudza zachwyt. W końcu kto z nas nie doceni piękna harmonii i równowagi?
Oto kilka przykładów zastosowania symetrii w sztuce i naturze:
- Obrazy renesansowe, które często korzystają z osi symetrii dla zharmonizowania kompozycji.
- Rosnące w naturalny sposób kwiaty, takie jak róże, które wykazują symetrię promienistą.
- Architektoniczne elementy, jak kolumny w świątyniach, które są zaprojektowane w symetryczny sposób.
- Wzory na muszlach, które ilustrują symetrię spiralną i osie symetrii.
| Rodzaj symetrii | Przykłady zastosowań |
|---|---|
| Symetria osiowa | Obrazy renesansowe, które korzystają z osi symetrii dla zharmonizowania kompozycji |
| Symetria promienista | Rosnące w naturalny sposób kwiaty, takie jak róże |
| Symetria w architekturze | Symetryczne elementy architektoniczne, jak kolumny w świątyniach |
| Symetria spiralna | Wzory na muszlach, ilustrujące symetrię spiralną i osie symetrii |
W naturze możemy dostrzec zjawisko nazywane "symetrią bilateralną", gdzie organizmy, takie jak motyle czy ryby, mają dwie identyczne połowy. Ciekawostką jest to, że niektóre stworzenia, jak na przykład kraby, mogą mieć asymetryczne cechy, co jest wynikiem adaptacji do środowiska, ale nadal zachowują pewne elementy symetrii w innych aspektach ich budowy.